mencari luas dan volume menggunakan integral

MENCARI volum MENGGUNAKAN INTEGRAL

Jika alas sebuah tabung dinyatakan dengan fungsi A(x) dan tinggi dari benda putar tersebut adalah panjang selang dari titik a ke b pada sumbu x atau y maka volume benda putar tersebut dapat dihitung dengan menggunakan rumus

V = ∫^b_a A(x) dx

Untuk mencari volume benda putar yang dihasilkan dari sebuah luasan yang diputar menurut sumbu x dan y dapat menggunakan cara seperti penjelasan berikut:

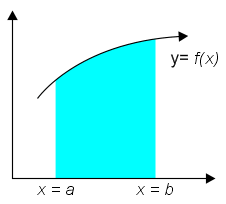
a. Volume Benda Putar terhadap Sumbu x yang dibatasi 1 Kurva

perhatikan gambar ilustrasi di atas. Luasan di bawah kurva y=f(x) jika diputar dengan sumbu putar dengan titik batas a dan b akan menghasilkan sebuah silinder dengan tinggi selisih b dan a. Volume benda putar menurut sumbu x tersebut dapat dicari dengan rumus

Contoh 1:
Hitung volume benda putar yang terbentuk jika daerah yang dibatasi oleh kurva y = x², sumbu x, dan 0 ≤ x ≤ 2 diputar terhadap sumbu x

Metode cakram:


Metode cincin silinder:
 

b. Volume Benda Putar terhadap Sumbu y yang dibatasi 1 Kurva

Untuk volume benda putar dengan sumbu putar adalah sumbu y, soba harus mengubah persamaan grafik yang semula y yang merupakan fungsi dari x menjadi kebalikannya x menjadi fungsi dari y.

y = f(x) menjadi x = f(y).

Misalkan
y = x²
x = √y

Setelah persamaan diubahf kebentuk x = f(y) kemudian dimasukkan ke rumus:

Contoh Soal

Tentukan volume dari benda putar jika daerah yang dibatasai oleh fungsi f(x) = 4 -x², sumbu x, dan sumbu y diputar 360º terhadap:

a. sumbu x
b. sumbu y

Jadi volume benda putar jika luasan M diputar mengelilingi sumbu x sebesar 360º adalah 256/15 π

b. Diputar mengelilingi sumbu y

Untuk mencari volume benda putarnya sobat harus menyatakan kurva y = f(x) = 4-x² menjadi bentuk persamaan x².
y = 4-x²
x² = 4-y
Luasan M memotong sumbu y di titik (0,0) dan (0,4)

Jadi jika luasan M diputar 360º derajat mengelilingi sumbu ya akan menghasilkan volume sebesar 8 π satuan volume.

Contoh 2:
Hitung volume benda putar yang terjadi bila daerah yang dibatasi oleh kurva y = x² dan garis y = 2x diputar mengelilingi sumbu y

Perpotongan kurva dan garis:
x² = 2x
x² – 2x = 0
x(x – 2) = 0
x = 0 atau x = 2
x = 0 → y = 0² = 0
x = 2 → y = 2² = 4
Jadi titik potong kurva dan garis adalah (0, 0) dan (2, 4)
Metode cakram:


Metode cincin silinder:

Contoh 3:
Jika daerah yang dibatasi oleh kurva x = (y – 2)² dan garis x + y = 4 diputar mengelilingi sumbu y, maka volume benda putar yang terjadi adalah …

Perpotongan kurva dan garis:
x + y = 4 → x = 4 – y
(y – 2)² = 4 – y
y² – 4y + 4 = 4 – y
y² – 4y + 4 – 4 + y = 0
y² – 3y = 0
y(y – 3) = 0
y = 0 atau y = 3
y = 0 → x = 4 – 0 = 4
y = 3 → x = 4 – 3 = 1
Jadi titik potong kurva dan garis (4, 0) dan (1, 3)
Metode cakram:


Metode cincin silinder:

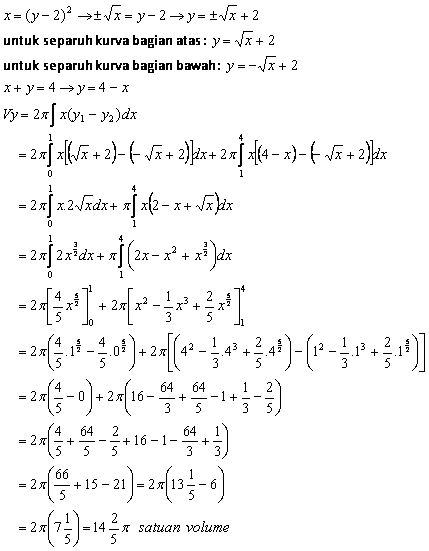
c. Volume Benda Putar yang Dibatasi Dua Kurva Jika Diputar Mengelilingi Sumbu x

Jika ada sebuah luasan yang dibatasi oleh dua kurva yaitu f(x) dan g(x) dimana |f(x)| ≥ |g(x)| dengan interval [a,b] diputar mengelilingi sumbu x, maka volume benda putar tersebut dapat dihitung dengan rumus:

 

c. Volume Benda Putar yang Dibatasi Dua Kurva Jika Diputar Mengelilingi Sumbu y

Sama prinsipnya dengan yang ada di huruf b, jika ada sebuah luasang yang terbentuk dari dua buah kurva x = f(y) dan x = g(y) dan interval [a.b] yang diputar mengitari sumbu y maka volume yang dihasilkan dapat dicari dengan rumus

Contoh Soal

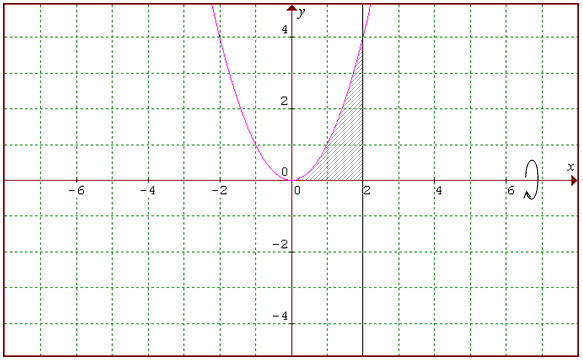
Hitunglah volume benda putar yang terjadi jika daereah yang dibatasi oleh kurva  y = √x , garis x = 2, garis y = 4, dan garis y = 3.

Jawab:

Kita gambar dulu luasan dimaksud

daerah berwarna biru muda di atas akan diputar mengelilingi sumbu x maka volume benda putar yang terjadi:

MENCARI LUAS MENGGUNAKAN INTEGRAL

Salah satu aplikasi integral tak tentu adalah untuk menghitung luas. Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva, di bawah kurva, di atas sumbu x ataupun di bawah sumbu x. Untuk itulah maka kita perlu memahami gambar kurva.
Untuk lebih jelasnya perhatikan kasus-kasus berikut

Jika kurva berada di bawah sumbu x maka metodanya adalah

Jika di antara dua kurva maka caranya sebagai berikut

Contoh soal 1

Tentukan luas daerah yang diarsir !


Jawab :

Contoh soal 2 :

Carilah luas daerah yang diarsir !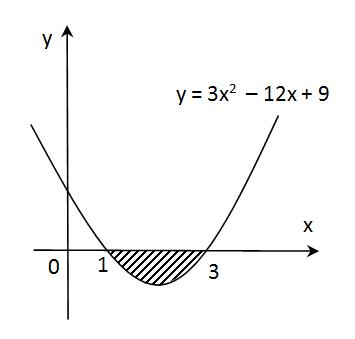
Jawab :


L = -3³ + 6.3² – 9.3 – (-1³ + 6.1² – 9.1)
L = -27 + 54 – 27 – (-1+ 6 – 9) = 0 – (-4) = 4

Contoh Soal 3 :

Luas daerah yang diarsir adalah …

Jawab :






Contoh Soal 4 :
Tentukan luas daerah yang diarsir berikut

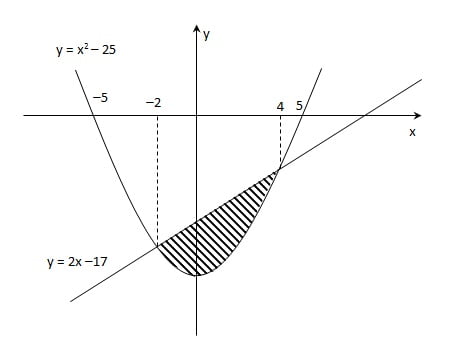
Jawab :
misalkan persamaan garis kita tulis menjadi f(x) = 2x – 17 dan parabola menjadi g(x) = x² – 25. Pada bagian yang diarsir, kurva f(x) lebih di atas dibandingkan dengan kurva g(x)
Maka luas daerah di atas bisa dinyatakan dengan

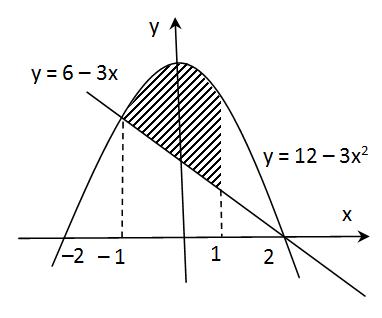
contoh 5:
Carilah luas yang diarsir dari gambar dibawah ini. Persamaan garisnya adalah dan .

Supaya lebih mudah, lebih baik kita menghitung luas kurva terhadap sumbu y. Sesuaikan persamaan kurva sehingga menjadi  dan , lalu cari titik potong nya.
     

    

Lakukan Integral dari kurva kanan dikurang kurva kiri. Gunakan batas integral dari -1 sampai 2.




















 Agar anda lebih mengerti lihatlah video dibawah ini.

agar anda lebih mengerti lihat video berikut ini